Московский государственный университет печати. §5 Теорема Гаусса Т гаусса

Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.

Зададим новую физическую величину, описывающую электрическое поле – поток Φ вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка Δ S .

Определение 1

Элементарный поток вектора напряженности (через площадку S) – это физическая величина, равная произведению модуля вектора E → , площади Δ S и косинуса угла α между вектором и нормалью к площадке:

Δ Φ = E Δ S cos α = E n Δ S.

В данной формуле E n является модулем нормальной составляющей поля E → .

Рисунок 1 . 3 . 1 . Иллюстрация элементарного потока Δ Φ .

Пример 1

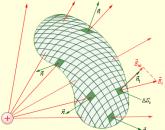
Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность S . Разобьем заданную поверхность на площадки небольшого размера Δ S i , рассчитаем элементарные потоки Δ Φ i поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток Φ вектора через замкнутую поверхность S (рис. 1 . 3 . 2):

Φ = ∑ ∆ Φ i = ∑ E m ∆ S i

Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.

Рисунок 1 . 3 . 2 . Расчет потока Ф через произвольную замкнутую поверхность S .

Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.

Теорема 1

Поток вектора напряженности электростатического поля E → через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε 0 .

Уравнение Гаусса имеет вид:

Φ = 1 ε 0 ∑ q в н у т р

Доказательство 1

Докажем указанную теорию: для этого исследуем сферическую поверхность (или поверхность шара) S . В центре заданной поверхности расположен точечный заряд q . Любая точка сферы обладает электрическим полем, перпендикулярным поверхности сферы и равным по модулю:

E = E n = 1 4 π ε 0 · q R 2 ,

где R является радиусом сферы.

Поток Φ через поверхность шара запишется, как произведение E и площади сферы 4 π R 2 . Тогда: Φ = 1 ε 0 q .

Следующим нашим шагом будет окружение точечного заряда произвольной поверхностью S замкнутого типа; зададим также вспомогательную сферу R 0 (рис. 1 . 3 . 3).

Рисунок 1 . 3 . 3 . Поток электрического поля точечного заряда через произвольную поверхность S , окружающую заряд.

Возьмем для рассмотрения конус с малым телесным углом Δ Ω при вершине. Рассматриваемый конус задаст на сфере малую площадку Δ S 0 , а на поверхности S – площадку Δ S . Элементарные потоки Δ Φ 0 и Δ Φ через эти площадки являются одинаковыми. В самом деле:

Δ Φ 0 = E 0 Δ S 0 , Δ Φ = E Δ S cos α = E Δ S " ,

где выражением Δ S " = Δ S cos α определяется площадка, которая задастся конусом с телесным углом Δ Ω на поверхности сферы радиуса n .

Поскольку ∆ S 0 ∆ S " = R 0 2 r 2 , то ∆ Φ 0 = ∆ Φ . Из полученного следует вывод о том, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ 0 через поверхность вспомогательной сферы:

Φ = Φ 0 = q ε 0 .

Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q , поток Φ равен нулю. Этот случай проиллюстрирован на рис. 1 . 3 . 2 . Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.

Обобщение теоремы Гаусса на случай произвольного распределения зарядов является следствием из принципа суперпозиции. Поле любого распределения зарядов возможно записать в виде векторной суммы электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S сложится из потоков Φ i электрических полей отдельных зарядов. Когда заряд q i расположен внутри поверхности S , он дает вклад в поток, равный q i ε 0 . В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.

Так, мы доказали теорему Гаусса.

Замечание 1

Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона .

Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).

Пример 2

В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R . Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l , закрытого с обоих торцов (рис. 1 . 3 . 4).

Рисунок 1 . 3 . 4 . Иллюстрация поля однородно заряженного цилиндра. O O " – ось симметрии.

Если r ≥ R , то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2 π r l . Применим закон Гаусса и получим:

Φ = E 2 π r l = τ l ε 0 .

В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:

E = τ 2 π ε 0 r .

Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.

Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r < R . В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ = E 2 π r l . Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.

Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.

Пример 3

К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).

При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.

Пример 4

Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис. 1 . 3 . 5).

Рисунок 1 . 3 . 5 . Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.

Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:

2 E ∆ S = σ ∆ S ε 0 или E = σ 2 ε 0 .

Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.

Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Закон взаимодействия электрических зарядов - закон Кулона - можно сформулировать иначе, в виде так называемой теоремы Гаусса. Теорема Гаусса получается как следствие закона Кулона и принципа суперпозиции. Доказательство основывается на обратной пропорциональности силы взаимодействия двух точечных зарядов квадрату расстояния между ними. Поэтому теорема Гаусса применима к любому физическому полю, где действует закон обратных квадратов и принцип суперпозиции, например к гравитационному полю.

Рис. 9. Линии напряженности электрического поля точечного заряда, пересекающие замкнутую поверхность X

Для того чтобы сформулировать теорему Гаусса, вернемся к картине силовых линий электрического поля неподвижного точечного заряда. Силовые линии уединенного точечного заряда представляют собой симметрично расположенные радиальные прямые (рис. 7). Можно провести любое число таких линий. Обозначим полное их число через Тогда густота силовых линий на расстоянии от заряда, т. е. число линий, пересекающих единицу поверхности сферы радиуса равна Сравнивая это соотношение с выражением для напряженности поля точечного заряда (4), видим, что густота линий пропорциональна напряженности поля. Мы можем сделать эти величины численно равными, надлежащим образом выбрав полное число силовых линий N:

Таким образом, поверхность сферы любого радиуса, охватывающей точечный заряд пересекает одно и то же число силовых линий. Это значит, что силовые линии непрерывны: в промежутке между любыми двумя концентрическими сферами разных радиусов ни одна из линий не обрывается и не добавляется ни одной новой. Поскольку силовые линии непрерывны, то такое же число силовых линий пересекает любую замкнутую поверхность (рис. 9), охватывающую заряд

Силовые линии имеют направление. В случае положительного заряда они выходят наружу из окружающей заряд замкнутой поверхности, как показано на рис. 9. В случае отрицательного заряда они входят внутрь поверхности. Если число выходящих линий считать положительным, а входящих - отрицательным, то в формуле (8) можно опустить знак модуля у заряда и записать ее в виде

Поток напряженности. Введем теперь понятие потока вектора напряженности поля через поверхность. Произвольное поле можно мысленно разбить на малые области, в которых напряженность меняется по модулю и направлению столь мало, что в пределах этой области поле можно считать однородным. В каждой такой области силовые линии представляют собой параллельные прямые и имеют постоянную густоту.

Рис. 10. К определению потока вектора напряженности поля через площадку

Рассмотрим, какое число силовых линий пронизывает малую площадку направление нормали к которой образует угол а с направлением линий напряженности (рис. 10). Пусть - проекция на плоскость, перпендикулярную силовым линиям. Так как число линий, пересекающих одинаково, а густота линий, согласно принятому условию, равна модулю напряженности поля Е, то

Величина а представляет собой проекцию вектора Е на направление нормали к площадке

Поэтому число силовых линий пересекающих площадку равно

Произведение носит название потока напряженности поля через поверхность Формула (10) показывает, что поток вектора Е через поверхность равен числу силовых линий, пересекающих эту поверхность. Отметим, что поток вектора напряженности, как и число проходящих через поверхность силовых линий, есть скаляр.

Рис. 11. Поток вектора напряженности Е через площадку

Зависимость потока от ориентации площадки относительно силовых линий иллюстрируется рис.

Поток напряженности поля через произвольную поверхность представляет собой сумму потоков через элементарные площадки, на которые можно разбить эту поверхность. В силу соотношений (9) и (10) можно утверждать, что поток напряженности поля точечного заряда через любую охватывающую заряд замкнутую поверхность 2 (см. рис. 9), как число выходящих из этой поверхности силовых линий равен При этом вектор нормали к элементарным площадкам замкнутой поверхности следует направлять наружу. Если заряд внутри поверхности отрицателен, то силовые линии входят внутрь этой поверхности и связанный с зарядом поток вектора напряженности поля также отрицателен.

Если внутри замкнутой поверхности находится несколько зарядов, то в соответствии с принципом суперпозиции будут складываться потоки напряженностей их полей. Полный поток будет равен где под следует понимать алгебраическую сумму всех зарядов, находящихся внутри поверхности.

Если внутри замкнутой поверхности электрических зарядов нет или их алгебраическая сумма равна нулю, то полный поток напряженности поля через эту поверхность равен нулю: сколько силовых линий входит в объем, ограниченный поверхностью, столько же и выходит наружу.

Теперь можно окончательно сформулировать теорему Гаусса: поток вектора напряженности электрического поля Е в вакууме через любую замкнутую поверхность пропорционален полному заряду находящемуся внутри этой поверхности. Математически теорема Гаусса выражается той же формулой (9), где под понимается алгебраическая сумма зарядов. В абсолютной электростатической

системе единиц СГСЭ коэффициент и теорема Гаусса записывается в виде

В СИ и поток напряженности через замкнутую поверхность выражается формулой

Теорема Гаусса широко используется в электростатике. В некоторых случаях с ее помощью легко рассчитываются поля, создаваемые симметрично расположенными зарядами.

Поля симметричных источников. Применим теорему Гаусса для расчета напряженности электрического поля равномерно заряженного по поверхности шара радиуса . Будем для определенности считать его заряд положительным. Распределение зарядов, создающих поле, обладает сферической симметрией. Поэтому такой же симметрией обладает и поле. Силовые линии такого поля направлены по радиусам, а модуль напряженности одинаков во всех точках, равноудаленных от центра шара.

Для того чтобы найти напряженность поля на расстоянии от центра шара, проведем мысленно концентрическую с шаром сферическую поверхность радиуса Поскольку во всех точках этой сферы напряженность поля направлена перпендикулярно ее поверхности и одинакова по модулю, то поток напряженности просто равен произведению напряженности поля на площадь поверхности сферы:

Но эту величину можно выразить и с помощью теоремы Гаусса. Если нас интересует поле вне шара, т. е. при то, например, в СИ и, сравнивая с (13), находим

В системе единиц СГСЭ, очевидно,

Таким образом, снаружи шара напряженность поля такая же, как у поля точечного заряда помещенного в центр шара. Если же интересоваться полем внутри шара, т. е. при то так как весь распределенный по поверхности шара заряд находится вне мысленно проведенной нами сферы. Поэтому поле внутри шара отсутствует:

Аналогично с помощью теоремы Гаусса можно рассчитать электростатическое поле, создаваемое бесконечной заряженной

плоскостью с плотностью постоянной во всех точках плоскости. По соображениям симметрии можно считать, что силовые линии перпендикулярны плоскости, направлены от нее в обе стороны и имеют всюду одинаковую густоту. Действительно, если бы густота силовых линий в разных точках была различной, то перемещение заряженной плоскости вдоль самой себя приводило бы к изменению поля в этих точках, что противоречит симметрии системы - такой сдвиг не должен изменять поле. Другими словами, поле бесконечной равномерно заряженной плоскости является однородным.

В качестве замкнутой поверхности для применения теоремы Гаусса выберем поверхность цилиндра, построенного следующим образом: образующая цилиндра параллельна силовым линиям, а основания имеют площади параллельны заряженной плоскости и лежат по разные стороны от нее (рис. 12). Поток напряженности поля через боковую поверхность равен нулю, поэтому полный поток через замкнутую поверхность равен сумме потоков через основания цилиндра:

Рис. 12. К вычислению напряженности поля равномерно заряженной плоскости

По теореме Гаусса этот же поток определяется зарядом той части плоскости, которая лежит внутри цилиндра, и в СИ равен Сравнивая эти выражения для потока, находим

В системе СГСЭ напряженность поля равномерно заряженной бесконечной плоскости дается формулой

Для равномерно заряженной пластины конечных размеров полученные выражения приближенно справедливы в области, находящейся достаточно далеко от краев пластины и не слишком далеко от ее поверхности. Вблизи краев пластины поле уже не будет однородным и его силовые линии искривляются. На очень больших по сравнению с размерами пластины расстояниях поле убывает с расстоянием так же, как поле точечного заряда.

В качестве других примеров полей, создаваемых симметрично распределенными источниками, можно привести поле равномерно заряженной по длине бесконечной прямолинейной нити, поле равномерно заряженного бесконечного кругового цилиндра, поле шара,

равномерно заряженного по объему, и т. п. Теорема Гаусса позволяет во всех этих случаях легко рассчитывать напряженность поля.

Теорема Гаусса дает связь между полем и его источниками, в некотором смысле обратную той, что дает закон Кулона, который позволяет определить электрическое поле по заданным зарядам. С помощью теоремы Гаусса можно определить суммарный заряд в любой области пространства, в которой известно распределение электрического поля.

В чем различие концепций дальнодействия и близкодействия при описании взаимодействия электрических зарядов? В какой мере эти концепции можно применить к гравитационному взаимодействию?

Что такое напряженность электрического поля? Что имеют в виду, когда ее называют силовой характеристикой электрического поля?

Каким образом по картине силовых линий можно судить о направлении и модуле напряженности поля в некоторой точке?

Могут ли силовые линии электрического поля пересекаться? Аргументируйте свой ответ.

Нарисуйте качественную картину силовых линий электростатического поля двух зарядов таких, что .

Поток напряженности электрического поля через замкнутую поверхность выражается разными формулами (11) и (12) в системах единиц ГСЭ и в СИ. Как это увязать с геометрическим смыслом потока, определяемого числом силовых линйй, пересекающих поверхность?

Как использовать теорему Гаусса для нахождения напряженности электрического поля при симметричном распределении создающих его зарядов?

Как применить формулы (14) и (15) к вычислению напряженности поля шара с отрицательным зарядом?

Теорема Гаусса и геометрия физического пространства. Посмотрим на доказательство теоремы Гаусса с несколько иной точки зрения. Вернемся к формуле (7), из которой был сделан вывод о том, что через любую окружающую заряд сферическую поверхность проходит одно и то же число силовых линий. Этот вывод связан с тем, что происходит сокращение в знаменателях обеих частей равенства.

В правой части возникло из-за того, что сила взаимодействия зарядов, описываемая законом Кулона, обратно пропорциональна квадрату расстояния между зарядами. В левой части появление связано с геометрией: площадь поверхности сферы пропорциональна квадрату ее радиуса.

Пропорциональность площади поверхности квадрату линейных размеров - это отличительная черта евклидовой геометрии в трехмерном пространстве. Действительно, пропорциональность площадей именно квадратам линейных размеров, а не какой-либо иной целой степени, характерно для пространства

трех измерений. То, что этот показатель степени равен точно двум, а не отличается от двойки пусть даже на ничтожно малую величину, свидетельствует о неискривленности этого трехмерного пространства, т. е. о том, что его геометрия именно евклидова.

Таким образом, теорема Гаусса - это проявление свойств физического пространства в фундаментальном законе взаимодействия электрических зарядов.

Идея о тесной связи фундаментальных законов физики со свойствами пространства высказывалась многими выдающимися умами еще задолго до установления самих этих законов. Так, И. Кант за три десятилетия до открытия закона Кулона писал о свойствах пространства: «Трехмерность происходит, по-видимому, оттого, что субстанции в существующем мире действуют одна на другую таким образом, что сила действия обратно пропорциональна квадрату расстояния».

Закон Кулона и теорема Гаусса фактически представляют один и тот же закон природы, выраженный в различных формах. Закон Кулона отражает концепцию дальнодействия, в то время как теорема Гаусса исходит из представления о силовом поле, заполняющем пространство, т. е. из концепции близкодействия. В электростатике источником силового поля является заряд, и связанная с источником характеристика поля - поток напряженности - не может измениться в пустом пространстве, где нет других зарядов. Поскольку поток можно наглядно представлять себе как совокупность силовых линий поля, то неизменность потока проявляется в непрерывности этих линий.

Теорема Гаусса, основанная на обратной пропорциональности взаимодействия квадрату расстояния и на принципе суперпозиции (аддитивности взаимодействия), применима к любому физическому полю, в котором действует закон обратных квадратов. В частности, она справедлива и для гравитационного поля. Ясно, что это не просто случайное совпадение, а отражение того, что и электрическое, и гравитационное взаимодействия разыгрываются в трехмерном евклидовом физическом пространстве.

На какой особенности закона взаимодействия электрических зарядов основана теорема Гаусса?

Докажите, основываясь на теореме Гаусса, что напряженность электрического поля точечного заряда обратно пропорциональна квадрату расстояния. Какие свойства симметрии пространства используются в этом доказательстве?

Каким образом геометрия физического пространства отражается в законе Кулона и теореме Гаусса? Какая особенность этих законов свидетельствует об евклидовом характере геометрии и трехмерности физического пространства?

Эта теорема представляет собой только следствие закона Кулона и принципа суперпозиции электрических полей. Вот её формулировка:

Поток вектора напряжённости электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме электрических зарядов, заключённых внутри этой поверхности, делённой на электрическую постоянную  0 .

Доказательство теоремы начнём с простейшего случая: вычислим поток вектора напряжённости поля точечного заряда Q .

Напряжённость этого поля хорошо известна (см. 1.3)

Учитывая сферическую симметрию поля, выберем вначале в качестве гауссовой замкнутой поверхности сферу радиусом r , с центром в той точке, где находится зарядQ (рис. 2.5., 1). Поток вектора напряжённости через эту поверхность вычислить легко

Здесь мы учли, что:

Рис. 2.5.

Учитывая последнее замечание, запишем поток (2.7) в следующем виде:

(2.8)

Таким образом, для первого простейшего случая теорема Гаусса оказалась справедливой. Что из этого следует?

Полученный результат позволяет заключить, что найденный поток не зависит от радиуса гауссовой поверхности. Это легко понять: ведь с увеличением расстояния от заряда Q площадь поверхностирастёт пропорционально квадрату радиуса, а напряжённость поляубывает обратно пропорционально квадрату радиуса.

Вспомним, кроме того, что поток вектора напряжённости равен числу силовых линий, пронизывающих гауссову поверхность. Независимость потока от радиуса поверхности означает, что силовые линии поля точечного заряда, начинаясь на положительном заряде, простираются далее до бесконечности, не прерываясь. Отсюда - дальнейшие выводы.

Поток вектора напряжённости поля точечного заряда через любую замкнутую поверхность (рис. 2.5, 2),охватывающую точечный заряд Q , равен отношению

Этот вывод несомненен, так как поток равен прежнему неизменному числу силовых линий, пронизывающий замкнутую поверхность.

Поток вектора напряжённости, через произвольную замкнутую поверхность, не охватывающую электрический заряд, равен нулю (рис. 2.5, 3).

Этот вывод также легко понять, так как число силовых линий втекающих в гауссову поверхность, равно числу линий, покидающих её. Поэтому суммарный поток через эту поверхность равен нулю.

Теперь можно обратиться к рассмотрению общего случая: пусть произвольная замкнутая поверхность S охватываетN точечных зарядов (рис. 2.6.). Вычислим поток вектора напряжённости суммарного поля через эту поверхностьS, учтя, что в соответствии с принципом суперпозиции результирующее поле равно векторной сумме отдельных полей

Рис. 2.6.

Итак, воспользовавшись определением потока, вычислим его через произвольную замкнутую поверхность S .

(2.9)

Полученный результат является доказательством справедливости теоремы Гаусса: поток вектора напряжённости электростатического поля в вакууме через любую замкнутую поверхность пропорционален алгебраической сумме зарядов, заключенных внутри этой поверхности .

Электростатическое поле – это особый вид материи, с помощью которой происходит взаимодействие заряженных тел.

Закон Кулона :сила взаимодействия F между двумя неподвижными точечными зарядами q 1 и q 2 прямопропорциональна величинам этих зарядов и обратно пропорциональна квадрату расстояния r между ними:

Где (e 0 – электрическая постоянная);

e – диэлектрическая проницаемость среды, показывающая во сколько раз сила взаимодействия зарядов в данной среде меньше, чем в вакууме.

Элект­рические поля, которые создаются неподвижными электрическими зарядами, называ­ются электростатическими .

Напряженность электростатического поля в данной точке есть физическая величина , определяемая силой, действующей на пробный точечный положительный заряд q 0 , помещенный в эту точку поля, то есть:

Электростатическое поле может быть изображено графически с помощьюсиловых линий .Силовая линия - это такая линия, касательная в каждой точке к которой совпадает по направлению с вектором напряженности электростатическго поля в данной точке (рис. 1, 2).

Если поле создается точечным зарядом, то силовые линии – это радиальные прямые, выходящие из положительного заряда (рис. 2, а ), и входя­щие в отрицательный заряд (рис. 2, б ).

Рис. 1 Рис. 2

С помощью силовых линий можно характеризовать не только направление, но и величину напряженности электростатического поля, связывая ей с густотой силовых линий. Большей густоте силовых линий соответствует большая величина напряженности (рис. 1, 2). Количественно числу силовых линий, прони­зывающих единичную площадку, расположенную перпендикулярно силовым линиям, ставится в соответствие величина напряженности электростатического поля. В этом случае определенному заряду q , создающему поле, соответствует определенное число N силовых линий, выходящих (для ) из заряда или входящих (для ) в заряд, а именно: .

Поток вектора напряженности электростатического поля через произвольную площадку S характкризуется числом силовых линий, пронизывающих данную площадку S.

Если площадка S перпендикулярна силовым линиям (рис. 3), то поток Ф Е вектора напряженности через данную площадку S : .

Рис. 3 Рис. 4

Рис. 3

Если же площадка S расположена неперпендикулярно силовым линиям электро-статического поля (рис. 4), то поток вектора через данную площадку S :

,

где α – угол между векторами напряженности и нормали к площадке S .

Для того, чтобы найти поток Ф Е вектора напряженности через произвольную поверхность S , необходиморазбить эту поверхность на элементарные площадки dS (рис. 5),определить элементарный поток dФ Е через каждую площадку dS по формуле:

,

а затем все эти элементарные потоки dФ Е сложить, что приводит к интегрированию:

,

где α – угол между векторами напряженности и нормали к данной элементарной площадке dS .

Если ввести вектор (рис. 5) как вектор, равный по величине площади площадки dS и направленный по вектору нормали к площадке dS , то величина , где a – угол между векторами и может быть записана в виде скалярного произведения векторов и , то есть, как , а полученное соотношение для потока вектора примет вид:

.

Теорема Остроградского - Гаусса для электростатического поля.

Теорема Остроградского - Гаусса для электростатического поля связывает между собой величину потока Ф Е вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность S с величинойзаряда q , заключенного внутри данной замкнутой поверхности S (рис. 6).

Рис. 6

Поскольку все силовые линии, выходящие из заряда (для ) или входящие в заряд (для ), пронизываютпроизвольную замкнутую поверхность S , охватывающую этот заряд (рис. 6), то величина потока Ф Е вектора через эту поверхность S будет определяться числом N силовых линий выходящих из заряда (для ) или входящих в заряд (для ):

.

Это соотношение есть теорема Остроградского-Гаусса для электростатического поля.

Таккак поток считается положитель­ным, если силовые линии выходят из поверхности S , и отрицательным для линий, входящих в поверхность S, то в случае, если внутри произвольной замкнутой поверхности S находится не один, а несколько (n ) разноименных зарялов, то теорема Остроградского - Гаусса для электростатического поля формулируется следующим образом:

поток вектора напряженности электростатического поля в вакууме через произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e 0 :

.

Тема 2. Работа сил электростатического поля. Потенциал

Если в электростатическом поле, создаваемом точечным зарядом q , перемещается другой пробный заряд q 0 из точки 1 в точку 2 вдоль произвольной траектории (рис. 7), то при этом совершается работа сил электростатического поля.

Элементарная работа dA силы на элементарном перемещении равна: .

Из рисунка 7 видно, что .

Тогда ().

Работа А при перемещении заряда q 0 вдоль траектории от точки 1 до точки 2 :

То есть работа при перемещении заряда из точки 1 в

точку 2 в электростатическом поле не зависит от траектории перемещения, а определяется только положениями начальной и конечной точек. Поэтому электростатическое поле точечного заряда является потенциальным .

Работа, совершаемая силами электростатического поля при перемещении заряда q 0 из точки 1 в точку 2 , выражается следующим образом:

,

где φ 1 и φ 2 – потенциалы электростатического поля в точках 1 и 2 .

Потенциал электростатического поля определяется с точностью до произвольной аддитивной постоянной С , то есть для поля точечного заряда q :

.

Тогда , .

Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами электростатического поля, при перемещении пробного точечного заряда q 0 из точки 1 в точку 2 :

.

Связь между напряженностью и потенциалом электростатического поля

Напряженность и потенциал φ электростатического поля связаны между собой следующим образом:

= – grad φ

или , где

– единичные векторы координатных осей Ох , Оy , Оz , соответственно.

Знак минус в приведенной формуле означает, что вектор напряженности электростатического поля направлен в сторону максимального убывания потенциала j .

Для графического изображения распределения потенциала электростатического поля используютсяэквипотенциальные поверхности, то естьповерхности, во всех точках которых потенциал j имеет одно и то же значение.

Например, для поля, созданного точечным зарядом q , потенциал j определяется выражением: , а эквипотенциальными поверхностями являются кон­центрические сферы (рис. 8).

Из этого рисунка видно, что в случае точечного заряда силовые линии поля (штриховые линии на рисунке) нормальны (перпендикулярны) к эквипотенциальным поверхностям (сплошные линии на рисунке).

Это свойство нормального взаимного расположения силовых линий и эквипотенциальных поверхностей электростатического поля является общим для любых случаев электростатического поля.

Таким образом, зная расположение силовый линий электростатического поля, можно построить эквипотенциальные поверхности этого электростатического поля и, наоборот, по известному расположению эквипотенциальных поверхностей электростатического поля можно построить силовые линии электростатического поля.

Магнитное поле

Тема 3. Магнитное поле. Закон Био-Савара-Лапласа

Электрический ток создает поле, действующее на магнитную стрелку. Стрелка ориентируется по касательной к окружности, лежащей в плоскости, перпендикуляной к проводнику с током (рис. 9).

Основной характеристикой магнитного поля является вектор индукция . Принято, что вектор индукция магнитного поля направлен в сторону север-ного полюса магнитной стрелки, помещенной в данную точку поля (рис. 9).

По аналогии с электрическим полем, магнитное поле также может быть изображено графически с помощью силовых линий (линий индукции магнитного поля ).

Силовая линия – это такая линия, касательная к которой в каждой точке совпадает по направлению с вектором индукции магнитного поля. Силовые линии магнитного поля, в отличие от силовых линий электростатического поля, являются замкнутыми и охватывают проводники с током. Направление силовых линий задается правилом правого винта (правилом буравчика): головка винта, ввинчиваемого по направлению тока, враща­ется в направлении линий Рис. 9

магнитной индукции (рис. 9).

Для нескольких источников магнитного поля согласно принципу суперпозиции магнитных полей индукция результирующего магнитного поля равна векторной сумме индукций всех отдельных магнитных полей:

Вектор индукции магнитного поля, создаваемого проводником с током , можно определить с помощью закона Био-Савара-Лапласа. При этомнеобходимо учесть то, что закон Био-Савара-Лапласа позволяет найти модуль и направление лишьвектора индукции магнитного поля, создаваемого элементом проводника с током . Поэтому для определения вектора индукции магнитного поля, создаваемого проводником с током , необходимо первоначально разбить этот проводник на элементы проводника , для каждого элемента с помощью закона Био-Савара-Лапласа найти вектор индукции , а затем, используя принцип суперпозиции магнитных полей, сложить векторно все найденные вектора индукции .

В ряде случаев теорема Гаусса позволяет найти напряженность электрического поля протяженных заряженных тел, не прибегая к вычислению громоздких интегралов. Обычно это относится к телам, чья геометрическая форма обладает определенными элементами симметрии (шар, цилиндр, плоскость). Рассмотрим некоторые примеры применения теоремы Гаусса для расчета напряженности электрических полей.

Пример 1 . Поле равномерно заряженной плоскости.

Электрическое поле, создаваемое бесконечно протяженной равномерно заряженной плоскостью, является однородным – в каждой точке пространства вне плоскости его напряженность всюду одинакова. Направлено это поле перпендикулярно к плоскости в обе стороны (рис.2.5). Поэтому для потока вектора напряженности поля через произвольно выбранную цилиндрическую поверхность, опирающуюся на элемент плоскости ΔS, можем написать: , откуда , где - поверхностная плотность заряда. Размерность в СИ: .

Таким образом, искомая напряженность электрического поля равномернозаряженной плоскости .

Пример 2 . Поле равномерно заряженной нити (цилиндра).

В данном случае электрическое поле обладает аксиальной симметрией – не зависит от азимутального угла φ и координаты z и направлено вдоль радиус-вектора (рис.2.6). Поэтому для потока вектора через выбранную цилиндрическую поверхность с осью, совпадающей с заряженной нитью, имеем: , где - элемент цилиндрической поверхности; l – длина произвольного участка нити.

С другой стороны, по теореме Гаусса этот поток равен: причем , - линейная плотность заряда нити. Отсюда находим: .

Искомая напряженность электрического поля равномерно заряженной нити : .

Пример 3 . Поле равномерно заряженного шара.

а) Металлический шар . При равновесии заряды равномерно распределяются по внешней поверхности заряженного шара (рис.2.7). Поэтому при < (внутри шара) электрическое поле отсутствует: .

Вне шара ( > ) электрическое поле, созданное равномерно распределенными по его поверхности зарядами, обладает сферической симметрией (направлено по радиальным линиям), поэтому, согласно теореме Гаусса:

.

Видим, что электрическое поле равномерно заряженного металлического шара не зависит от радиуса шара и совпадает с полем точечного заряда .

б) Диэлектрический шар .

Рассмотрим шар, с условной диэлектрической проницаемостью ε = 1, равномерно заряженный по объему с плотностью заряда (рис.2.8).

Размерность объемной плотности заряда в СИ: .

Полный заряд шара, очевидно, есть: .

Имеем по теореме Гаусса:

1) Внутри шара (r < R) : , где Δq = - заряд внутренней области шара, ограниченной выбранной сферической поверхностью радиуса r . Отсюда находим: .

2) Вне шара (r > R) : , откуда = ,

то есть вне заряженного диэлектрического шара электрическое поле такое же , как и в случае металлического шара.

На рис.2.9 показан качественный ход зависимостей E(r) для металлического и диэлектрического шаров.

металл Рис.2.9 . Зависимость E(r). диэлектрик

1.4 Теорема Гаусса. Вектор электрической индукции.

Теорема Гаусса.

Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя теорему Гаусса, определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность .

Рассмотрим поток вектора напряженности через сферическую поверхность радиуса r , охватывающую точечный заряд q , находящийся в ее центре

Этот результат справедлив для любой замкнутой поверхности произвольной формы ,охватывающей заряд.

Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю ,так как число линий напряженности,входящих в поверхность,равно числу линий напряженности, выходящих из нее.

Рассмотрим общий случай произвольной поверхности, окружающей n зарядов .Согласно принципу суперпозиции напряженностьполя ,создаваемого всеми зарядами, равна сумме напряженностей , создаваемых каждым зарядом в отдельности. Поэтому

Теорема Гаусса для электростатического поля в вакууме :потоквектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленных на ε 0 .

В общем случае электрические заряды могут быть распределены с некоторой объемной плотностью , различной в разных местах пространства. Тогда суммарный заряд объема V, охватываемого замкнутой поверхностью S равен и теорему Гаусса следует записать в виде .